At ValidExamDumps, we consistently monitor updates to the CFA Institute CFA-Level-II exam questions by CFA Institute. Whenever our team identifies changes in the exam questions,exam objectives, exam focus areas or in exam requirements, We immediately update our exam questions for both PDF and online practice exams. This commitment ensures our customers always have access to the most current and accurate questions. By preparing with these actual questions, our customers can successfully pass the CFA Institute CFA Level II Chartered Financial Analyst exam on their first attempt without needing additional materials or study guides.
Other certification materials providers often include outdated or removed questions by CFA Institute in their CFA Institute CFA-Level-II exam. These outdated questions lead to customers failing their CFA Institute CFA Level II Chartered Financial Analyst exam. In contrast, we ensure our questions bank includes only precise and up-to-date questions, guaranteeing their presence in your actual exam. Our main priority is your success in the CFA Institute CFA-Level-II exam, not profiting from selling obsolete exam questions in PDF or Online Practice Test.
Carol Blackwell, CFA, has been hired to manage trust assets for Blanchard Investments. Blanchard's trust manager, Thaddeus Baldwin, CFA, has worked in the securities business for more than 50 years. On Blackwell's first day at the office, Baldwin gives her several instructions.
Instruction 1: Limit risk by avoiding stock options.
Instruction 2: Above all, ensure that our clients' capital is kept safe.
Instruction 3: We take pride in our low cost structure, so avoid unnecessary transactions.
Instruction 4: Remember that every investment must have the quality to stand on its own.
Baldwin realizes that many of the firm's practices and policies would benefit from a compliance check. Because Blackwell recently received her CFA charter, Baldwin tells her she is the "perfect person to work with the compliance officer to update the policy on proxy voting and the procedures to comply with Standard VI(B) Priority of Transactions." Baldwin also wants Blackwell to evaluate whether the firm wants to, or can, claim compliance with the soft dollar standards. Baldwin hands Blackwell a handwritten outline he created, which includes the following statements:
Statement 1: CFA Institute's soft-dollar rules are not mandatory. In any case, ' client brokerage can be used to pay for a portion of mixed-use research.
Statement 2: Investment firms can use client brokerage to purchase research that does not immediately benefit the client. Commissions generated by outside trades are considered soft dollars, but commissions from internal trading desks are not.
During a local society luncheon, Blackwell is seated next to CFA candidate Lucas Walters, who has been assigned the task of creating a compliance manual for Borchard & Sons, a small brokerage firm. Walters asks for her advice.
When Walters returns to work, he is apprised of the following situation: Borchard & Sons purchased 25,000 shares of CBX Corp. for equity manager Quintux Quantitative just minutes before the money manager called back and said it meant to buy 25,000 shares of CDX Corp. Borchard then purchased CDX shares for Quintux, but not before shares of CBX Corp. declined by 1.5%. The broker is holding the CBX shares in its own inventory.
Borchard proposes three methods for dealing with the trading error.
Method 1: Quintux directs additional trades to Borchard worth a dollar value equal to the amount of the trading loss.
Method 2: Borchard receives investment research from Quintux in exchange for Borchard covering the costs of the trading error.
Method 3: Borchard transfers the ordered CBX shares in its inventory to Quintux, which allocates them to all of its clients on a pro-rata basis.
Are Thaddeus Baldwin's statements on the soft dollar standards correct?
Commissions from both internal and external brokerage operations are considered soft dollars, so Statement 2 is false. Statement 1 is true. CFA Institute Soft Dollar Standards are voluntary, though firms that wish to claim compliance with the Standards must follow them completely. Client brokerage can be used to pay for mixed-use research with the caveat that the research must be reasonable, justifiable, and documcntable, and that the client brokerage is only used to pay for the portion of the research that will be used in the investment decision-making process. While research paid for by client brokerage should directly benefit the client, it does not have to do so immediately. (Study Session 1, LOS 3-b)
Yi Tang updates several economic parameters monthly for use by the analysts and the portfolio managers at her firm. If economic conditions warrant, she will update the parameters even more frequently. As a result of an economic slowdown, she is going through this process now.
The firm has been using an equity risk premium of 5.6%, found with historical estimates. Tang is going to use an estimate of the equity risk premium found with a macroeconomic model. By comparing the yields on nominal bonds and real bonds, she estimates the inflation rate to be 2.6%. She expects real domestic growth to be 3.0%. Tang does not expect a change in price/earnings ratios. The yield on the market index is 1.7% and the expected risk-free rate of return is 2.7%.
Elizabeth Trotter, one of the firm's portfolio Managers, asks Tang about the effects of survivorship bias on estimates of the equity risk premium. Trotter asks, "Which method is most susceptible to this bias, historical estimates, Gordon growth model estimates, or survey estimates?"
Tang wishes to estimate the required rate of return for Northeast Electric (NE) using the Capital Asset Pricing Model (CAPM) and the Fama-French three factor model. She is using the following information to accomplish this:
* The risk-free rate of return is 2.7%.
* The expected risk premiums arc:
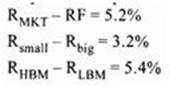
* The beta coefficient in the CAPM is estimated to be 0.63.
* The betas (factor sensitivities) for the three Fama-French factors are 1.00 for the market factor, -0.76 for the size factor, and -0.04 for the book-to-markct factor.
Trotter also asks Tang about adjusted betas. She says, "We use a formula for the adjusted beta where the adjusted beta = (2/3) (regression beta) + (1/3) (1.0). How do the adjusted betas compare to the original regression betas?"
Trotter has one final question for Tang. Trotter says, "We need to estimate the equity beta for VixPRO, which is a private company that is not publicly traded. We have identified a publicly traded company that has similar operating characteristics to VixPRO and we have estimated the beta for that company using regression analysis. We used the return on the public company as the dependent variable and the return on the market index as the independent variable. What steps do I need to take to find the beta for VixPRO equity? The companies have different debt/equity ratios. The debt of both companies is very low risk, and I believe I can ignore taxes."
The estimate of the equity risk premium found with a macroeconomic model and the estimates determined by Tang is closest to:
The equity risk premium is estimated as:

where
i = the inflation rate = 2.6%
REg = expected real growth in GDP = 3.0%
PEg = relative value changed due to changes in P/E ratio = 0
Y = yield on the market index = 1.7%
RF = risk-free rate of return = 2.9%
ERP = (1.026) x (1.030) x (1.00)-1 +0.017-0.027 = 0.04678 = 4
(Study Session 10, LOS 35.b)
Jenna Stuart is a financial analyst for Deuce Hardware Company, a U .S . company that reports its results in U .S . dollars. Wayward Distributing, Inc., is a foreign subsidiary of Deuce Hardware, which began operations on January 1,2007. Wayward is located in a foreign country and reports its results in the local currency called the Rho. Selected balance sheet information for Wayward is shown in the following table.
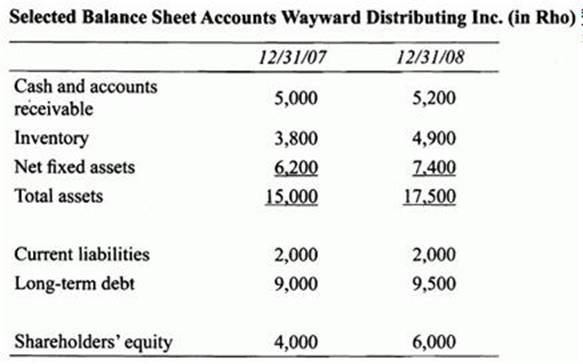
Stuart has been asked to analyze how the reported financial results of Wayward will be affected by the choice of the all-current or temporal methods of accounting for foreign operations. She has gathered the following exchange rate information on the $/Rho exchange rate:
* Spot rate on 1/01/08: $0.35 per Rho
* Spot rate on 12/31/08: $0.45 per Rho
* Average spot rate during 2008: $0.42 per Rho
Will total asset turnover (calculated using end-of-period balance sheet figures) likely be larger when calculated from the Rho financial statements or the financial statements translated into the reporting currency (US$) using the all-current method?
If the Rho is appreciating, mixed ratios like return on assets and total asset turnover (using end-of-pcriod balance sheet figures) calculated from the local currency statements will be larger than the same ratios calculated from the reporting currency statements that were translated using the all-current method. For example, under the all-current method net income will be translated at the lower average rate ($0.42) and assets will be rramlared at the higher ending rate ($0.45). Therefore the original return on assets (ner income divided by total assets) from the Rho statements will be higher than the ratio after it is translated into the reporting currency. (Study Session 6, LOS 23.d,e)
Frank Hoskins and Paul Lanning are economists for a large U .S . investment advisory firm. Platinum Advisors. Hoskins and Lanning use their independent research on U .S . stocks and international stocks to provide advice for the firm's network of advisors. As the senior economist at Platinum, Hoskins is a partner in the firm and is Lanning's supervisor. Lanning has worked for Platinum for the past four years. At a lunch meeting, the two economists discuss the usefulness of economic theory, economic data, and the resulting forecasts of the global economic and stock market activity.
Hoskins is investigating the growth prospects of the country of Maldavia. Maldavia is a formerly communist country with a population of 3 million located in Eastern Europe. The Maldavian government had been aggressive in instituting political reform and encouraging the growth of financial markets. However, due to a recent insider trading scandal and resulting stock market volatility, the Maldavian government is considering restrictions on further stock market growth and the establishment of a national securities regulator. Hoskins states that these developments are not encouraging for future economic growth.
Lanning is examining the country of Petra. Petra is a country of 25 million located in South America and rich with natural resources including oil. The recently elected president of Petra, Carlos Basile, has announced that he would like to diversify the country's economy away from natural resources while nationalizing the oil industry. Lanning states that these changes would not be beneficial for the future growth of the Petrian economy.
One of the many items they study when examining an economy or stock market is the economic information released by governments and private organizations. Hoskins and Lanning use this information to determine the effects on economic growth and the appropriate portfolio allocations to the bond and stock markets. Examining information for Maldavia, Hoskins has learned that the Maldavian private sector has embarked on an ambitious plan to increase labor productivity by purchasing more machinery for its factories. The private sector feels compelled to do this because Maldavia has historically relied too heavily on labor as the main input into production. Plotting the productivity curve for Maldavia, Hoskins states that labor productivity should increase because the productivity curve will shift upward and to the right.
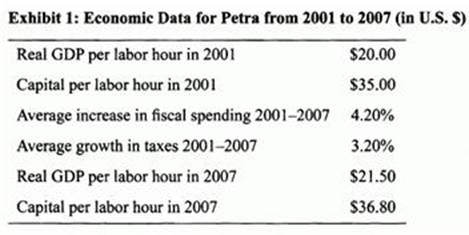
Lanning is examining the historical record of economic growth in Petra. He has gathered the data in Exhibit 1 to determine potential economic growth.
Hoskins is also examining data for the country of Semeria. Semeria is an emerging country that has benefited from recent changes in the political environment as well as technological advances. Its economy is growing rapidly, and changes in the Semerian economy and society have resulted in more opportunities for women. The Semerian economy has experienced 17 consecutive quarters of positive growth in GDP, which is unprecedented in Semerian history. Interest rates have increased over time because businesses have been borrowing heavily to invest in new machinery and technologies. Most economists are forecasting further increases in interest rates in Semeria.
It has long been Platinum's policy that its economists use long-term economic growth trends to forecast future economic growth, stock returns, and dividends in a country. Lanning is examining the economy of Tiberia. Tiberia has a population of 11 million and is located in northern Africa. Its economy is diversified, and its main exports are agricultural products and heavy machinery. The country's economy has been growing at an annual rate of 6.2% for the past ten years, in part because of technological advances in the manufacture of heavy equipment. These advances involve the use of computer-operated welding machines that have made the manufacture of heavy equipment less expensive. Lanning is worried, however, that the 6.2% GDP growth rate may not be sustainable and is considering advising Platinum's portfolio managers to decrease their portfolio allocations in the country. Before doing so, he will consult with Hoskins.
The endogenous growth theory is most likely to predict that the Tiberian dividend growth rate:
Under the endogenous growth theory, the Tibcrian dividend growth rate can continue to increase because technological advances will be shared by many sectors of the economy. The benefits of technological advances cannot be captured entirely by a single firm. As these benefits flow to other firms, the economy becomes more productive and the long-term economic growth rate and dividend growth rate can continue to increase. Under the endogenous growth theory, the economy does not necessarily settle at a long-run equilibrium growth rate as it docs under the neoclassical model, which posits a diminishing marginal productivity of capital. (Study Session 4, LOS 14.f)
Russell Larson, CFA, is an investment analyst for Sentry Properties, Inc., a group of wealthy investors that is currently interested in purchasing Riviera Terrace, a 60- unit apartment complex in Southeastern Florida. The current owners of Riviera Terrace have agreed to sell the property for $40,000,000. Larson estimates that Rivjera Terrace's net operating income for the first year after the sale is finalized will be $4,200,000, and it is expected to maintain its historic annual growth rate of 5%.
At Sentry's request, Larson will evaluate the investment in Riviera Terrace over a 5-year horizon using selling prices of $45,000,000 and S60,000,000.
During the due diligence process, Larson has determined that the average selling price for apartment complexes similar to Riviera Terrace is $1,250,000 per unit, with annual net operating income equal to $ 135,000 per unit. Larson has also determined that net operating income is typically 80% of gross income.
Larson has collected the following information to aid in his evaluation of Riviera Terrace.
* The property will be fully depreciated at a rate of S 1,250,000 per year over 32 years.
* Rental contracts are expected to be reissued on the date the sale is completed.
* Sentry has arranged to finance the investment with a 30-ycar, 7% interest-only loan, with monthly payments and a face value equal to 80% of the initial investment.
* Selling expenses will be 7% of the gross selling price.
* The capital gains tax rate is 15%, the tax on recaptured depreciation is 28%, and the tax rate on ordinary income is 40%.
* Sentry Properties' required return on equity is 20%.
* The interest rate on U .S . government bonds after adjustments for real estate based tax savings = 5.0%.
* The premium investors require for the illiquidity of real estate investments = 2.5%.
* The average real estate return net of appreciation = 1.25%.
* The real estate investment risk premium = 3.0%.
* The average internal rate of return for properties that are comparable to Riviera Terrace is 22%.
As part of the diligence process, Larson deems it to be appropriate to estimate the.market value of Riviera Terrace using capitalization rates based on the market extraction and built-up methods. One of the partners in Sentry Properties has also asked Larson to estimate the market value of Riviera Terrace using: (1) the direct income capitalization approach and (2) the gross income multiplier approach.
There are several indicators that the Florida real estate market may take a downward turn over the next five years. With this in mind, Larson determines that there is a reasonable chance that Sentry will have to terminate its investment in Riviera Terrace at the end of year 3 at the initial purchase price of $40,000,000. Under this scenario, he estimates the equity reversion after tax (ERAT) in year 3 to be $4,934,000. Cash flow after tax in years 1 and 2 are $1,676,000 and $1,802,000, respectively.
In the scenario in which Sentry will sell Riviera Terrace for $45,000,000 at the end of the investment horizon, the equity reversion after tax is closest to:
